Analysis of Frequency and Bandwidth Performance Grading Problems in General Cabling of Communication Channels

“Let’s take a look at some of the principles behind the ability of communication channels to convey information, as well as data encoding techniques.Since there are some theoretical and mathematical calculations that will be covered here, I will try to avoid complex math problems as much as possible, but it is impossible to completely ignore them.

“

Let’s take a look at some of the principles behind the ability of communication channels to convey information, as well as data encoding techniques. Since there are some theoretical and mathematical calculations to be covered here, I will try to avoid complex math problems as much as possible, but it is impossible to ignore them completely.

1. Application of coding technology

In fact, Shannon’s formula has long outlined the relationship between bandwidth B and rate C: C=B*Log(1+SNR) where B is the channel bandwidth, and the so-called bandwidth refers to the frequency range that can transmit signals with appropriate fidelity , whose unit is Hz, is inherent in the channel itself and has nothing to do with the carried signal. SNR is the signal-to-noise ratio, which is jointly determined by the transmitting and receiving equipment of the system and the electromagnetic environment in which the transmission system is located. The rate C is a calculation result, which is jointly determined by B and SNR, and its unit is bps, which is conceptually represented as the number of bits transmitted per second.

It can be seen that, given the channel, the bandwidth B is also given, and different transmission rates C can be obtained by changing the signal-to-noise ratio SNR. MHz has a one-to-many relationship with Mbps, that is, the same bandwidth can transmit different bit stream rates. Meanwhile, Mbps is application-dependent; MHz is application-independent.

If you want to give it an image metaphor, then the car speed and engine speed are just right. Given the rotational speed, the speed of the car can be calculated given the gears. In this analogy, the gear acts as a bridge. In fact, gears are to cars and engines what encoding systems are to speed and bandwidth.

Coding is used for information transmission by computers. By encoding the information, many technical problems such as synchronization, limited bandwidth, etc. can be solved. Coding is critical for the reliable transmission of information.

There are currently two basic encoding families. The first is to add a synchronization bit every N bits to make synchronization possible (such as Manchester encoding when N=1; 4B5B encoding when N=4), but this requires a more large bandwidth. And the more sync bits, the larger the bandwidth needs. In order to reduce bandwidth, it is possible to use an encoding system that adds a synchronization bit every 7 bits (i.e. 7B8B encoding), but it follows that when transmitting a longer stream of the same type of bit stream, the synchronization becomes very difficult.

Another coding series reduces the bandwidth by increasing the number of levels. The more levels, the less bandwidth is required. However, when transmitting a long sequence of continuous signals encoded by zeros, synchronization becomes nearly impossible. For example, when we use 5 levels, we need 4 comparators, and each comparator should have its proper tolerance range. That said, when we choose the total number of levels, we should also take the signal-to-noise ratio (SNR) into account in order to be able to identify these different levels.

Manchester (Manchester), NRZ1 (non-return-to-zero coding) and MLT-3 (three-level bipolar) coding are the three main coding systems currently used. Their transfer factors are 1, 0.5 and 0.25, respectively. These transition factors can be defined as a ratio of MHz pairs. From this point of view, any encoding system has its technical limitations. In addition, there are some parameters such as DC components that also impose certain restrictions on encoding. In practical applications, the current major encoding systems are used in combination to make a compromise between bandwidth and synchronization, or have some emphasis. For example, a pair of For applications with high synchronization requirements, Manchester encoding system or other encoding methods that can generate timing can be selected. For another example, a 100 Mbps application using MLT-3 encoding requires a bandwidth of 25 MHz; when the 4B5B encoding method is used in combination, the system needs to add an additional 25 Mbps overhead, and the entire system requires a bandwidth of 31.25 MHz. Synchronization just got easier. In addition, it is worth mentioning that 100 Fast Ethernet uses a 5B6B encoding system (IEEE802.13), which can be said to be a typical example of a compromise between bandwidth and synchronization.

2. Basic principles

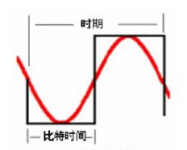
Simply put, data communication on a local area network is accomplished by sending a series of ‘1’s and ‘0’ codes from a transmitter to a receiver. Binary data is usually represented as a square wave (Figure 1).
　　

However, what is transmitted on the twisted pair is not a pure square wave. Binary data is essentially a repeated form (at one point). The repeated form 101010 represents the worst-case model. Fourier transform shows[Note: Fourier transform has a wide range of applications in physics, number theory, combinatorics, signal processing, probability theory, statistics, cryptography, acoustics, optics, oceanography, structural dynamics, etc. (For example in signal processing, a typical use of the Fourier transform is to decompose a signal into amplitude and frequency components). ]this worst-case repeating form does consist of a finite series of sinusoidal frequency components (sine waves) that can be divided into a fundamental frequency and a large number of harmonics (several fundamental frequencies). It’s a bit like a circle is made up of a finite number of very short straight lines. The fundamental frequency is a sine wave with a period equal to twice the bit time. This sounds very complicated and we can explain it better with a simplified example: bit time = 1/bit rate So if the 101010 form is part of a 10Mbps data stream, we have 10,000,000 bits per second . Each bit occupies ten millionths of a second. The period of the fundamental frequency is twice the bit time (see Figure 1), or two ten-millionths of a second. Fundamental frequency = 1/cycle = 5,000,000 Hz = 5 MHz (Hz = cycles/second).

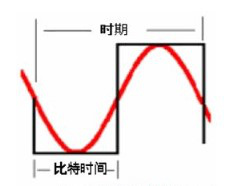
To get a reasonable square wave, the fundamental frequency must be supplemented by harmonics (odd harmonics only in the case of the square wave above). To get a perfect square wave, there must also be a finite number of such harmonics. Since an active device handles a reasonable approximation of a square wave, the fundamental plus the third and fifth harmonics (or in some cases the fundamental plus the third) is sufficient.
　

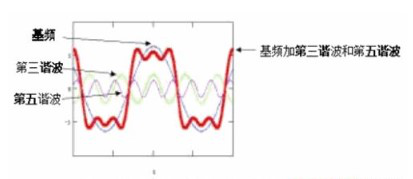
The sum of the waveforms that can be seen in Figure 2 is a relatively close representation of the sequence of “0” and “1”. The effects of crosstalk and attenuation tend to affect the waveform as well. This begins to explain why 10Base-T at 10Mbps per second requires 16MHz of bandwidth for Category 3 cabling, a 5MHz fundamental plus a 15MHz third harmonic.

3. Practical application

The bandwidth of a communication system expresses its ability to transmit these different frequency components. The unit of bandwidth in structured cabling systems is usually expressed in MHz. The bandwidth of Category 5e cabling is nominally 100MHz. Assuming the application of a simple binary transmission “code”, then theoretically, the maximum information transmission rate can be calculated by the Nyquist equation: C= 2 W Log 2 M where W is the bandwidth (unit: H z ), M is the number of signaling units, when M=2, C=2W.

This results in a theoretical information capacity of 2 x 108 bits per second, or 200 Mbps. In practice, this value is reduced due to the effects of crosstalk and attenuation.

Then, the super five types of information channels support data transmission up to Gigabit Ethernet (1000Mbps), how to make the bandwidth suitable for it? Then the data transmission rate must be increased, and the key to increasing the data throughput is to introduce more than 1 bit per signaling unit. Most public protocols in commercial use use this technique to some extent, which we call data encoding.

Most data encoding types are implemented using mBnL encoding, that is, a sequence of m bits is represented by n pulses at each level of L levels. Examples are ISDN and Fast Ethernet. Take 100Base-T4 as an example. The 100 Mbps signal is transmitted in three pairs. The bit rate per pair is 33.33 Mbps. To reduce the frequency capacity of the bit stream and the bandwidth requirements of the wiring system, triple coding is used. Before transmitting each group of 8-bit data, it is converted into 6 triple symbols (see Figure 3).
　

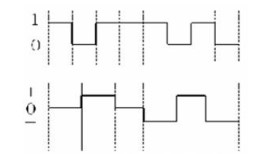
This reduces the effective clock rate of the transmit signaling system to 25 MHz, which reduces (in the first example we described) the fundamental frequency to 12.5 MHz. This allows transmission rates of 100 Mbps within the bandwidth provided in a Category 3 cabling system.

Gigabit Ethernet uses a different scheme that converts groups of 8 bits (8 B) of data into four quintuples (1 Q 4) transmissions across four twisted pairs, each symbol Represents two binary bits or zero. That is, using PAM-5 encoding, it uses five levels of -2, -1, 0, 1, and 2, of which four levels are used for user signal encoding, and one level is used for forward error correction encoding. Compared with binary coding, the five-level PAM coding doubles the channel utilization, so that the signal baud rate per line pair is reduced to 125MB/s, and the baseband will be 62.5MHz, which reduces the bandwidth occupied by the signal again. This ensures that the Category 5e system meets the bandwidth requirements.

4. Conclusion

The bit rate of each application is related to its base frequency. The highest frequency capacity is the harmonics of the fundamental frequency. It should not be confused with clock frequency (the bit stream is sampled at the clock frequency). For example, 10Base-T has a bit rate of 10Mbps and a sampling clock of 10MHz, but the base frequency is only 5MHz. By expressing system performance requirements in MHz, the standard provides a blueprint upon which active network component designers can design their equipment. Provided that the cabling system and active equipment meet the performance requirements of the relevant standards, then everything is running normally! As a user, the most interesting thing is the communication rate. Rates describe communications at the application level. In order to improve the communication rate, there are two ways to consider: one is to improve the transmission performance of the cable system, which determines the bandwidth; the other is to choose an appropriate encoding system, which determines the conversion factor. Although the bandwidth is physically limited, higher communication rates can be achieved with a suitable encoding system. In particular, it should be pointed out that the encoding system is application-dependent, which means that a new application with the same bit stream rate but different encoding methods may not be supported by the original system. Considering those cabling components that support existing application systems, and choosing a bit stream rate of MHz to describe, then this will lead to seriously wrong decisions. From this perspective, any open system should be independent of applications. And only use MHz to describe the communication rate, we can make adequate choices from the current and future broad application fields. For the performance grading of the integrated wiring system, we can only measure it with the bandwidth but not with the speed.